Explanation:
For this problem, you should use the equation
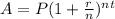 . For this problem, A=1800, P=1400, n=4, r=x, t=9.
. For this problem, A=1800, P=1400, n=4, r=x, t=9.
A = Final Amount
P = Principal (Original Amount)
n = Number of times it is compounded in a year. (Quarterly = 4)
r = Interest Rate (In the equation, you must convert your final answer to percent form)
t = Amount of years