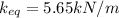Question

When a 75.0-kg man slowly adds his weight to a vertical spring attached to the ceiling, he reaches equilibrium when the spring is stretched by 6.50 cm. (a) Find the spring constant. (b) If a second, iden- tical spring is hung on the first in series, and the man again adds his weight to the system, by how much does the system of springs stretch? (c) What would be the spring constant of a single, equivalent spring?

Answer 1

1)
`k=11.319kN/m`

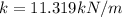
2)displacement
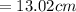
`=13.02cm`

3)
`k_(eq)=5.65kN/m`

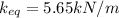
Step-by-step explanation:

At equilibrium position the weight of the man should be balanced by force in the spring

thus we have at equilibrium

`kx=mg\\\\k=(mg)/(x)`

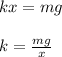
Applying values we get

`k=(75* 9.81)/(0.065)\\\\k=11.319kN/m`

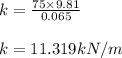
2)

When we add another identical spring we get an equivalent spring with spring constant as

`(1)/(k_(eq))=(1)/(k_1)+(1)/(k_2)`

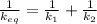
Applying values we get

`(1)/(k_(eq))=(1)/(11.319)+(1)/(11.319)\\\\k_(eq)=5.65kN/m`

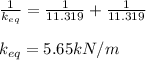
Thus at equilibrium we have

`x_(2)k_(eq)=mg\\\\x_(2)=(mg)/(k_(eq))\\\\x_(2)=(75* 9.81)/(5.65)* 10^(-3)=13.02cm`

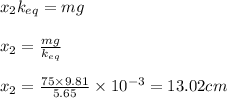
3) Equivalent spring constant will be as calculated earlier
`k_(eq)=5.65kN/m`