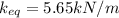Answer:
1)
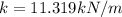
2)displacement
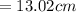
3)
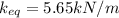
Step-by-step explanation:
At equilibrium position the weight of the man should be balanced by force in the spring
thus we have at equilibrium
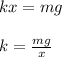
Applying values we get
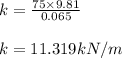
2)
When we add another identical spring we get an equivalent spring with spring constant as
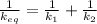
Applying values we get
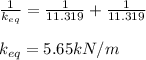
Thus at equilibrium we have
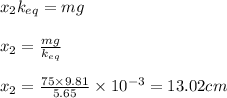
3) Equivalent spring constant will be as calculated earlier