Question

A flywheel in the form of a uniformly thick disk of radius 1.33 m1.33 m has a mass of 70.6 kg70.6 kg and spins counterclockwise at 217 rpm217 rpm . Calculate the constant torque required to stop it in 2.75 min2.75 min .

Answer 1

The constant torque required to stop the disk is 8.6 N-m in clockwise direction .

Step-by-step explanation:

Let counterclockwise be positive direction and clockwise be negative direction .

Given

Radius of disk , r = 1.33 m

Mass of disc , m = 70.6 kg

Initial angular velocity ,
`\omega_i =217 rpm`

Final angular velocity ,
`\omega_f =0\, rpm`

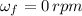
Time taken to stop , t = 2.75 min

Let
`\alpha` be the angular acceleration

We know

`\omega _f=\omega _i+\alpha t`

=>
`0=217+2.75\alpha =>\alpha = -78.9(rev)/(min^(2))`

=>
`\alpha =-(78.9* 2\pi)/(60* 60)(rad)/(s^(2))=-0.138 (rad)/(s^(2))`

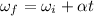
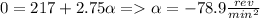
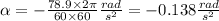
Torque required to stop is given by

`\tau =I\alpha`

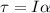
where moment of inertia ,
`I=(mr^(2))/(2)=(70.6* 1.33^(2))/(2)kg.m^(2)=62.5 kg.m^(2)`

=>
`\therefore \tau =-0.138* 62.5\, N.m=-8.6\, N.m`

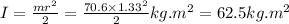
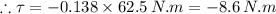
Thus the constant torque required to stop the disk is 8.6 N-m in clockwise direction .