Answer:
The constant torque required to stop the disk is 8.6 N-m in clockwise direction .
Step-by-step explanation:
Let counterclockwise be positive direction and clockwise be negative direction .
Given
Radius of disk , r = 1.33 m
Mass of disc , m = 70.6 kg
Initial angular velocity ,
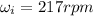
Final angular velocity ,
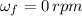
Time taken to stop , t = 2.75 min
Let
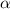 be the angular acceleration
be the angular acceleration
We know
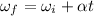
=>
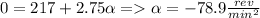
=>
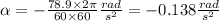
Torque required to stop is given by
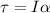
where moment of inertia ,
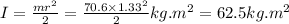
=>
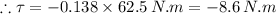
Thus the constant torque required to stop the disk is 8.6 N-m in clockwise direction .