Explanation:
It is given that,
Inductance,
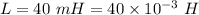
RMS value of voltage,

Frequency, f = 60 Hz
We need to find the energy stored at t = (1 /185) s. It is assumed that energy stored in the inductor is zero at t = 0. So,
The current flowing through the inductor is given by :
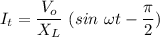
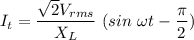
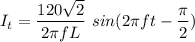
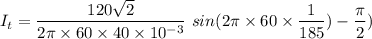

I = 0.091 A
Energy stored in the inductor is,
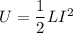
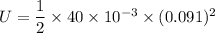
U = 0.000165 Joules
Hence, this is the required solution.