Question

If a series converges, then the sequence of partial sums of the series also converges. True False Submit Answer 10. –/1 points My Notes If a series an converges, then the terms an tend to zero as n increases. True False

Answer 1

True

True

Explanation:

We are given that a series converges

We have to check that if series converges then the sequence of partial sum converges

Let
`\sum_(k=1)^(n)a_n=L`

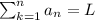
Because series converges

We have to show that
`\sum_(k=1)^(n-1)a_n=L`

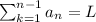
When series converges then the nth term tends to zero.It is a sufficient condition .

Then
`\sum_(k=1)^(n)a_n=a_n+\sum_(k=1)^(n-1)a_n`

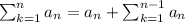
L=0+
`\sum_(k=1)^(n-1)a_n`

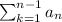
Hence,
`\sum_(k=1)^(n-1)a_n=L`

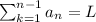
Therefore, if a series converges then the sequence of partial sum also converges is true.

If a series converges then the nth term tends to zero as n increases .It is a sufficient condition for series convergence .Hence, the statement is true.