Answer:
True
True
Explanation:
We are given that a series converges
We have to check that if series converges then the sequence of partial sum converges
Let
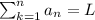
Because series converges
We have to show that
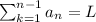
When series converges then the nth term tends to zero.It is a sufficient condition .
Then
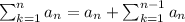
L=0+
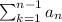
Hence,
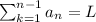
Therefore, if a series converges then the sequence of partial sum also converges is true.
If a series converges then the nth term tends to zero as n increases .It is a sufficient condition for series convergence .Hence, the statement is true.