Question

A speaker that emits sound is located at the origin of a coordinate system. Two microphones are located on the x-axis, with microphone 1 at the x = 3.0 meter mark and microphone 2 at the x = 5.0 meter mark. If the speed of sound is 343 m/s, how much longer does it take a sound emitted by the speaker to reach microphone 2 than microphone 1?

Answer 1

0.00583 seconds

Step-by-step explanation:

Distance from mic 1 to origin = 3 m

Distance from mic 2 to origin = 5 m

Speed of sound = 343 m/s

Time taken by mic 1

`t_1=\frac{\text{Distance from mic 1 to origin}}{\text{Speed of sound}}\\\Rightarrow t_1=(3)/(343)=0.008746\ s`

`t_2=\frac{\text{Distance from mic 2 to origin}}{\text{Speed of sound}}\\\Rightarrow t_2=(5)/(343)=0.014577\ s`

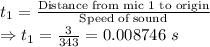
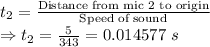
Time difference = t₂ - t₁ = 0.14577-0.008746 = 0.00583 s

∴ Difference in time taken by the speaker is 0.00583 s