Question

The monthly electrical utility bills of all customers for the Far East Power and Light Company are known to be normally distributed with mean equal to $87.00 a month and standard deviation of $36.00. If a statistical sample of n = 100 customers is selected at random, what is the probability that the average bill for those sampled will exceed $75.00? g

Answer 1

Answer: 0.9996

Explanation:

Given : The monthly electrical utility bills of all customers for the Far East Power and Light Company are known to be normally distributed with a mean
`\mu=$\ 87.00`

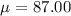
Standard deviation :
`\sigma=$\ 36.00`

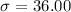
Sample size : n=100

Let X be the random variable that represents the electricity utility bill for a randomly selected month .

z-score :
`z=(X-\mu)/((\sigma)/(√(n)))`

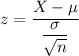
For X = $75.00

`z=(75.00-87.00)/((36)/(√(100)))\approx-3.33`

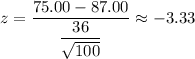
Now, the probability that the average bill for those sampled will exceed $75.00 will be :-

`P(X>75)=P(z>-3.33)=1-P(z\leq-3.33)\\\\=1-  0.0004342=0.9995658\approx0.9996`

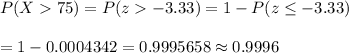
Hence, the probability that the average bill for those sampled will exceed $75.00 =0.9996