Answer: 0.9996
Explanation:
Given : The monthly electrical utility bills of all customers for the Far East Power and Light Company are known to be normally distributed with a mean
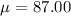
Standard deviation :

Sample size : n=100
Let X be the random variable that represents the electricity utility bill for a randomly selected month .
z-score :
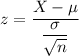
For X = $75.00
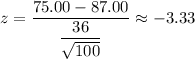
Now, the probability that the average bill for those sampled will exceed $75.00 will be :-
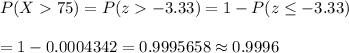
Hence, the probability that the average bill for those sampled will exceed $75.00 =0.9996