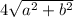Question

Help 15 pts. Please answer asap

Answer 1

The answer is D.

Explanation:

Answer 2

D.
`4\sqrt{a^(2)+b^(2)}`

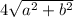
Explanation:

We can see the shape can be cut into 4 right triangles. We can use pythagoreans theorem to find the length of the hypotenuse.

The distance from 0 to a represents one side, and the distance from 0 to b represents the other side.

So

`a^(2) +b^(2) =C^(2)`

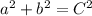
(C represents the hypotenuse)

So the hypotenuse can be written as
`\sqrt{a^(2) +b^(2) }`

Since four of these lines make up the perimeter,

the total perimeter will be
`4\sqrt{a^(2)+b^(2)}`