Question

Two strings have the same length and tension. One string has a mass per length that is 4 times that of the other string. The fundamental frequency of the more massive string will be times _________ (a) larger, (b) smaller than that of the less massive string.

Answer 1

`f_1=(f_2)/(2)`

Step-by-step explanation:

the Frequency of string is given by

`f= (1)/(2l)*\sqrt{(T)/(\mu )}`

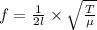
T= tension in the string

μ= mass per unit length of string

l= length of string

in the given question
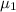`\mu_(1)`= 4
`\mu_(2)`

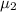
here subscript 1 is massive string and subscript 2 is lighter string

`f_(1)= (1)/(2l)*\sqrt{(T)/(\mu_(1) )}`

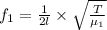
and

`f_(2)= (1)/(2l)*\sqrt{(T)/(\mu_(2) )}`

dividing f_1 by f_2 we get

now
`(f_(1))/(f_(2)) =\sqrt{(\mu_2)/(\mu_1) }`

=
`\sqrt{(\mu_2)/(4\mu_2) }`

=
`(1)/(2)`

⇒
`f_1=(f_2)/(2)`

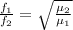
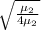
hence the fundamental frequency of massive string is half of the fundamental frequency of lighter string