Answer:
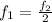
Step-by-step explanation:
the Frequency of string is given by
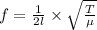
T= tension in the string
μ= mass per unit length of string
l= length of string
in the given question
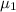 = 4
= 4
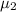
here subscript 1 is massive string and subscript 2 is lighter string
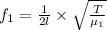
and
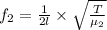
dividing f_1 by f_2 we get
now
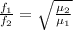
=
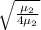
=
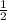
⇒
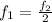
hence the fundamental frequency of massive string is half of the fundamental frequency of lighter string