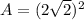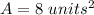Question

The coordinates of the vertices of a regular polygon are given. Find the area of the polygon to the nearest tenth.

A(0, 0), B(2, -2), C(0, -4), D(-2, -2)

Answer 1

The area is equal to
`8\ units^(2)`

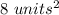
Explanation:

we have

A(0, 0), B(2, -2), C(0, -4), D(-2, -2)

Plot the figure

The figure is a square (remember that a regular polygon has equal sides and equal internal angles)

see the attached figure

The area of the square is

`A=AB^(2)`

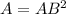
Find the distance AB

the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

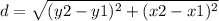
substitute the values

`AB=\sqrt{(-2-0)^(2)+(2-0)^(2)}`

`AB=\sqrt{(-2)^(2)+(2)^(2)}`

`AB=√(8)`

`AB=2√(2)\ units`

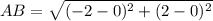
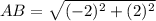
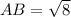
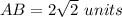
Find the area of the square

`A=(2√(2))^(2)`

`A=8\ units^(2)`