Answer: (4,-3)
Explanation:
When we shift a function g(x) , c units to the right , then the new function is given by :-

When we compare functions f(x) and f(x-5), we find that f(x-5) is the function which comes after a 5 units rightwards shift in f(x).
Also, The minimum point on the graph of the equation y=f(x) is (−1,−3).
The translation rule to move a point rightwards by d units:-
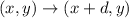
Using the above translation rule , we have
The minimum point on the graph of the equation
 as:
as:
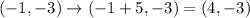
Hence, the minimum point on the graph of the equation
 =(4,-3)
=(4,-3)