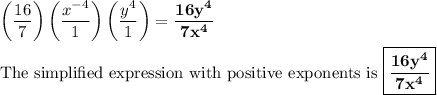Question

(7x^2y-2)^-1/(4x^-1y)^-2

Answer 1

`\boxed{(16y^(4))/(7x^(4))}`

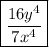
Explanation:

Your expression is

`((7x^(2)y^(-2))^(-1))/((4x^(-1)y)^(-2))`

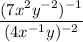
1. Handle the outer exponents

Remember that x⁻¹ = 1/x . Then

`((7x^(2)y^(-2))^(-1))/((4x^(-1)y)^(-2)) = ((4x^(-1)y)^(2))/(7x^(2)y^(-2))`

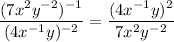
2. Square the numerator

When you square a number, you multiply its exponent by 2.

`((4x^(-1)y)^(2))/(7x^(2)y^(-2)) = (4^(2)x^(-2)y^(2))/(7x^(2)y^(-2))`

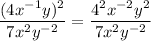
3. Divide like terms

`(4^(2)x^(-2)y^(2))/(7x^(2)y^(-2)) = \left ( (16)/(7)\right)\left ((x^(-2))/(x^(2))\right )\left ((y^(2))/(y^(-2))\right )`

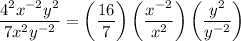
4. Evaluate each term

When you divide numbers with exponents, you subtract the exponent in the denominator from that in the numerator

`\left ( (16)/(7)\right)\left ((x^(-2))/(x^(2))\right )\left ((y^(2))/(y^(-2))\right ) = \left ( (16)/(7)\right)\left ((x^(-4))/(1)\right )\left ((y^(4))/(1)\right )`

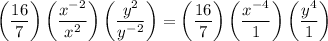
5. Move x to the denominator and combine terms

`\left ( (16)/(7)\right)\left ((x^(-4))/(1)\right )\left ((y^(4))/(1)\right ) =\mathbf{ (16y^(4))/(7x^(4))}\\\\\text{The simplified expression with positive exponents is } \boxed{\mathbf{(16y^(4))/(7x^(4))}}`