Answer:
(2,-3) and (-2,5)
Explanation:
Let us graph the two equations one by one.
1.

If we compare this equation with the slope intercept form of a line which is given as
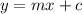
we see that m = -1 and c =1
Hence the slope of the line is -2 and the y intercept is 1. Hence one point through which it is passing is (0,1) .
Let us find another point by putting x = 1 and solving it for y


Let us find another point by putting x = 2 and solving it for y

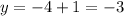
Hence the another point will be (2,-3)
Let us find another point by putting x = -2 and solving it for y
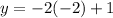
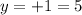
Hence the another point will be (-2,5)
Now we have two points (0,1) ,(1,-1) , (2,-3) and (-2,5) we joint them on line to obtain our line
2.
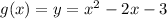
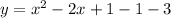
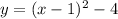
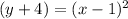
It represents the parabola opening upward with vertices (1,-4)
Let us mark few coordinates so that we may graph the parabola.
i) x=0 ;
 ; (0,-3)
; (0,-3)
ii)x=-1 ;
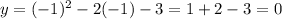 ; (-1,0)
; (-1,0)
iii) x=2 ;
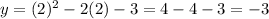 ;(2,-3)
;(2,-3)
iii) x=1 ;
 ;(1,-4)
;(1,-4)
iii) x=-2 ;
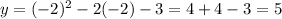 ;(-2,5)
;(-2,5)
Now we plot them on coordinate axis and line them to form our parabola
When we plot them we see that we have two coordinates (2,-3) and (-2,5) are common , on which our graphs are intersecting. These coordinates are solution to the two graphs.