Answer with Step-by-step explanation:
Let A, B and C are arbitrary sets within a universal set U.
We have to prove that
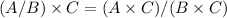 is always true.
is always true.
Let

Then
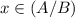 and
and
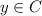
Therefore,
 and
and
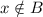
Then, (x,y) belongs to

and (x,y) does not belongs to

Hence,
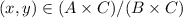
Conversely ,Let (x ,y)belongs to

Then
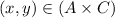 and
and
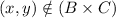
Therefore,
 and
and

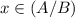 and
and
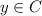
Hence,
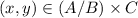
Therefore,
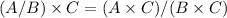 is always true.
is always true.
Hence, proved.