Question

Given: y" - 2y' = 6t + 5e^2t. Find the correct form to use for y_p if the equation is solved using Undetermined coefficients. Do NOT Solve the equation

Answer 1

`y_p=A+Bt+Ce^(2t)`

Explanation:

Given:
`y'' - 2y' = 6t + 5e^(2t)`.

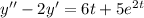we need to find the correct form for
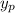`y_p` if the equation is solve using undetermined coefficients.

A first order differential equation
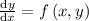`\frac{\mathrm{d} y}{\mathrm{d} x}=f\left ( x,y \right )` is said to be homogeneous if
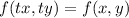`f(tx,ty)=f(x,y)` for all t.

Consider homogeneous equation
`y''-2y'=0`

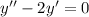
Let
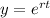`y=e^(rt)` be the solution .

We get
`(r^2-2r)e^(rt)=0`

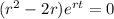
Since
`e^(rt)\\eq 0`,
`r^2-2r=0`.

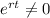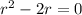So, we get solution as
`y_c=c_1+c_2e^(2t)`

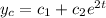
As constant term and
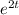`e^(2t)` are already in the R.H.S of equation

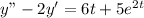`y`, we can take
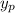`y_p` as
`y_p=A+Bt+Ce^(2t)`