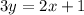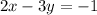Answer:
Part 1)
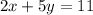
Part 2)
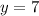
Part 3)
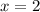
Part 4)
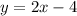
Part 5)
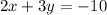
Part 6)
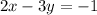
Explanation:
Part 1) Write the standard form of the line that passes through the given points
(3, 1) and (-2, 3)
we know that
The equation of the line in standard form is equal to
Ax+By=C
where
A is a positive integer
B and C are integers
step 1
Find the slope m
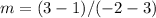

step 2
Find the equation in point slope form
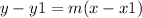
we have
 and point
and point
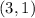
substitute
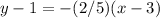
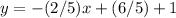
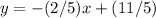
Convert to standard form
Multiply by 5 both sides
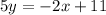
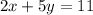 -----> equation in standard form
-----> equation in standard form
Part 2) Write the standard form of the line that passes through the given points
(4, 7) and (0, 7)
we know that
The equation of the line in standard form is equal to
Ax+By=C
where
A is a positive integer
B and C are integers
step 1
Find the slope m
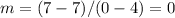
This is a horizontal line (parallel to the x-axis)
The equation of the line is
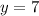
Part 3) Write the standard form of the line that passes through the given points
(2, 3) and (2, 5)
we know that
The equation of the line in standard form is equal to
Ax+By=C
where
A is a positive integer
B and C are integers
step 1
Find the slope m
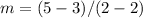
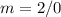 ----> the slope is undefined
----> the slope is undefined
This is a vertical line (parallel to the y-axis)
The equation of the line is
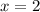
Part 4) Write the slope-intercept form of the line with a slope of 2 and a y -intercept of -4.
we know that
The equation of the line into slope-intercept form is equal to
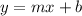
where
m is the slope and b is the y-intercept
we have
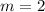
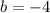
substitute
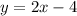
Part 5) Write the standard form of the line that is parallel to 2 x + 3 y = 4 and passes through the point (1, -4).
we know that
If two lines are parallel, then their slopes are the same
we have
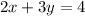
isolate the variable y
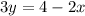
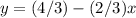
The slope of the given line is

so
Find the equation of the line with slope m=-2/3 and passes through the point (1,-4)
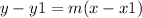
substitute
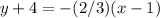
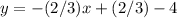
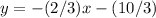
Convert to standard form
Multiply by 3 both sides
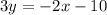
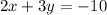
Part 6) Write the standard form of the line that contains a slope of 2/3 and passes through the point (1, 1)
Find the equation in point slope form
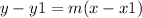
we have
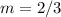 and point
and point
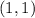
substitute
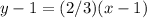
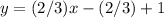
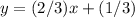
Multiply by 3 both sides