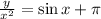Answer:
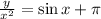
Explanation:
Consider linear differential equation
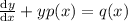
It's solution is of form
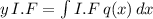 where I.F is integrating factor given by
where I.F is integrating factor given by
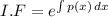 .
.
Given:
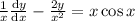
We can write this equation as
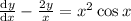
On comparing this equation with
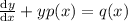 , we get
, we get
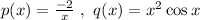
I.F =
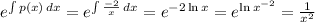 { formula used:
{ formula used:
 }
}
we get solution as follows:
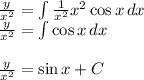
{ formula used:
 }
}
Applying condition:

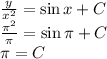
So, we get solution as :