Solve x'=5t(sqrt(x)) x(0)=1

Question

asked Dec 25, 2020 129k views

1 Answer

Luca Del Tongo · Answer 1 · 2020-12-30T00:16:00+0000

Answer:

2√(x)=(5t^2)/(2)+2

Explanation:

Given:
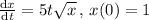
$\frac{\mathrm{d} x}{\mathrm{d} t}=5t√(x)\,,\, x(0)=1$

Solution:

A differential equation is said to be separable if it can be written separately as functions of two variables.

Given equation is separable.

We can write this equation as follows:

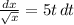
$(dx)/(√(x))=5t\,dt$

On integrating both sides, we get

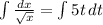
$\int (dx)/(√(x))=\int 5t\,dt$

Formulae Used:

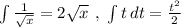
$\int (1)/(√(x))=2√(x)\,\,,\,\,\int t\,dt=(t^2)/(2)$

So, we get solution as
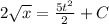
2√(x)=(5t^2)/(2)+C

Applying condition: x(0) = 1, we get
C=2

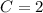
Therefore,
2√(x)=(5t^2)/(2)+2