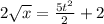Question

Solve x'=5t(sqrt(x)) x(0)=1

Answer 1

`2√(x)=(5t^2)/(2)+2`

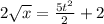
Explanation:

Given:
`\frac{\mathrm{d} x}{\mathrm{d} t}=5t√(x)\,,\, x(0)=1`

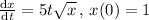
Solution:

A differential equation is said to be separable if it can be written separately as functions of two variables.

Given equation is separable.

We can write this equation as follows:

`(dx)/(√(x))=5t\,dt`

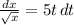
On integrating both sides, we get

`\int (dx)/(√(x))=\int 5t\,dt`

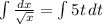
Formulae Used:

`\int (1)/(√(x))=2√(x)\,\,,\,\,\int t\,dt=(t^2)/(2)`

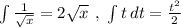
So, we get solution as
`2√(x)=(5t^2)/(2)+C`

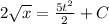
Applying condition: x(0) = 1, we get
`C=2`

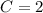
Therefore,
`2√(x)=(5t^2)/(2)+2`