Question

What is k if : k!+48=48((k+1)^m)

Answer 1

The value of k is greater than or equal to 0, i.e. k≥7.

Explanation:

The given equation is

`k!+48=48((k+1)^m)`

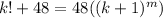
The value of k must be a positive integer because k! is defined for k≥0, where k∈Z.

Subtract 48 from both the sides.

`k!=48((k+1)^m)-48`

`k!=48((k+1)^m-1)`

`k!=48(k+1-1)(((k+1)^m-1)/((k+1)-1))`

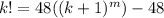
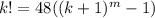
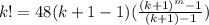
Using
`[(r^m-1)/(r-1)=r^(m-1)+r^(m-2)+...+1]`, we get

`k!=48k((k+1)^(m-1)+(k+1)^(m-2)+...+1)`

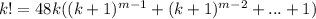
Divide both sides by 48k.

`(k!)/(48k)=(k+1)^(m-1)+(k+1)^(m-2)+...+1`

`(k(k-1)!)/(48k)=(k+1)^(m-1)+(k+1)^(m-2)+...+1`

`((k-1)!)/(48)=(k+1)^(m-1)+(k+1)^(m-2)+...+1`

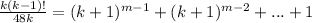
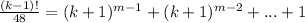
Note: The value of m can be 0 or 1.

The value of k is positive integer, so the right hand side of the above equation must be a positive integer.

Since RHS of the equation is positive integer, therefore (k-1)! is completely divisible by 48.

`k-1\geq 6`

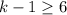
Add 1 on both sides.

`k\geq 6+1`

`k\geq 7`

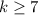
Therefore the value of k is greater than or equal to 0.