Answer:
The probability that a survey polling 5 people reveals that at most 2 voters support the candidate is 0.08704.
Explanation:
Given : Suppose that 60% of the voters in a state intend to vote for a certain candidate.
To find : What is the probability that a survey polling 5 people reveals that at most 2 voters support the candidate.
Solution :
Applying binomial probability distribution,
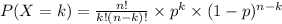
Here n=5 number of people
p=60%=0.6 probability of success.
k is at most 2 i.e.
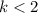
So, Probability is
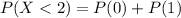
The probability for k=0.
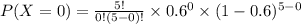
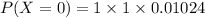
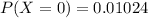
The probability for k=1.
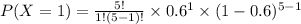

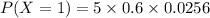
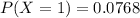
Substitute in
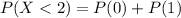
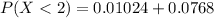
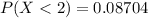
Therefore, The probability that a survey polling 5 people reveals that at most 2 voters support the candidate is 0.08704.