Question

Suppose that 60​% of the voters in a state intend to vote for a certain candidate. What is the probability that a survey polling 5 people reveals that at most 2 voters support the candidate.

Answer 1

The probability that a survey polling 5 people reveals that at most 2 voters support the candidate is 0.08704.

Explanation:

Given : Suppose that 60​% of the voters in a state intend to vote for a certain candidate.

To find : What is the probability that a survey polling 5 people reveals that at most 2 voters support the candidate.

Solution :

Applying binomial probability distribution,

`P(X=k)=(n!)/(k!(n-k)!)* p^k* (1-p)^(n-k)`

Here n=5 number of people

p=60%=0.6 probability of success.

k is at most 2 i.e.
`k<2`

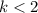
So, Probability is
`P(X<2)=P(0)+P(1)`

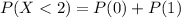
The probability for k=0.

`P(X=0)=(5!)/(0!(5-0)!)* 0.6^0* (1-0.6)^(5-0)`

`P(X=0)=1* 1* 0.01024`

`P(X=0)=0.01024`

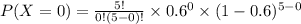
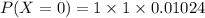
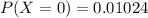
The probability for k=1.

`P(X=1)=(5!)/(1!(5-1)!)* 0.6^1* (1-0.6)^(5-1)`

`P(X=1)=(5* 4!)/(4!)* 0.6* 0.0256`

`P(X=1)=5* 0.6* 0.0256`

`P(X=1)=0.0768`

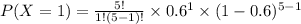
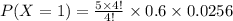
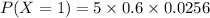
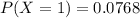
Substitute in
`P(X<2)=P(0)+P(1)`

`P(X<2)=0.01024+0.0768`

`P(X<2)=0.08704`

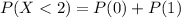
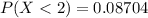
Therefore, The probability that a survey polling 5 people reveals that at most 2 voters support the candidate is 0.08704.

Answer 2

Answer: 0.31744

Explanation:

Binomial probability distribution formula :-

`P(X)=^nC_x \ p^x\ (1-p)^(n-x)`, where P(x) is the probability of getting success in x trials, n is total number of trials and p is the probability of getting succes in each trial.

Given : The probability that the voters in a state intend to vote for a certain candidate:
`p=0.60`

Now, the probability that a survey polling 5 people reveals that at most 2 voters support the candidate will be :-

`P(x\leq2)=P(0)+P(1)+P(2)\\\\=^5C_0 \ (0.60)^0\ (0.40)^(5)+^5C_1 \ (0.60)^1\ (0.40)^(4)+^5C_2 \ (0.60)^2\ (0.40)^(3)\\\\=(0.40)^5+5(0.60)(0.40)^4+10(0.60)^2(0.40)^3=0.31744`

Hence, the probability that a survey polling 5 people reveals that at most 2 voters support the candidate = 0.31744