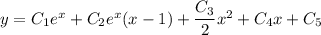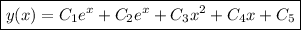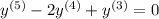
We can reduce the order of the ODE by substituting
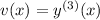 , so that
, so that
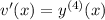 and
and
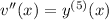 . Then
. Then
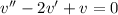
has characteristic equation
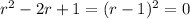
with root
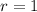 , which has multiplicity 2, so that the characteristic solution is
, which has multiplicity 2, so that the characteristic solution is
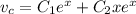
Integrate both sides to solve for
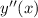 :
:
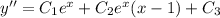
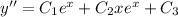
Integrate again to solve for
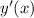 :
:
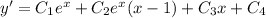
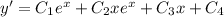
And one last time to solve for
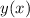 :
: