Answer:
The expression
![\sqrt[3]{16x^(7) } * \sqrt[3]{12x^(9) }](https://img.qammunity.org/2020/formulas/mathematics/middle-school/6ud8ripdrxohsujtf1zr75aw1vidtndz95.png) =
=
![4x^(5)} (\sqrt[3]{3x})](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ce97cb7f1g7xdjxxe3htxarltibl2v8vma.png)
Explanation:
Given
![\sqrt[3]{16x^(7) } * \sqrt[3]{12x^(9) }](https://img.qammunity.org/2020/formulas/mathematics/middle-school/6ud8ripdrxohsujtf1zr75aw1vidtndz95.png)
Required
Products of both
To do this, we have to apply the laws of indices,
Follow the highlighted steps
Step 1: Multiply both parameters directly
Since they both have the same roots, they can be multiplied directly according to the law of indices
![\sqrt[3]{16x^(7) } * \sqrt[3]{12x^(9) }](https://img.qammunity.org/2020/formulas/mathematics/middle-school/6ud8ripdrxohsujtf1zr75aw1vidtndz95.png) becomes
becomes
![\sqrt[3]{16x^(7) * 12x^(9) }](https://img.qammunity.org/2020/formulas/mathematics/middle-school/jf7y9mjxknxgbu5g84glwuthbcvfj16lbk.png)
Step 2: Apply the 1st law of indices
First law of indices states that
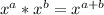
So,
![\sqrt[3]{16x^(7) * 12x^(9) }](https://img.qammunity.org/2020/formulas/mathematics/middle-school/jf7y9mjxknxgbu5g84glwuthbcvfj16lbk.png) becomes
becomes
![\sqrt[3]{16x^(7) * 12x^(9) }](https://img.qammunity.org/2020/formulas/mathematics/middle-school/jf7y9mjxknxgbu5g84glwuthbcvfj16lbk.png) =
=
![\sqrt[3]{16 * 12 * x^(7) * x^(9) }](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ft9xha6iqimdfe1wb9cyfcw3f25d01azeh.png)
![\sqrt[3]{16x^(7) * 12x^(9) }](https://img.qammunity.org/2020/formulas/mathematics/middle-school/jf7y9mjxknxgbu5g84glwuthbcvfj16lbk.png) =
=
![\sqrt[3]{16 * 12 * x^(7+9) }](https://img.qammunity.org/2020/formulas/mathematics/middle-school/9axewj0tx0qdul2uog45n25ng6qh7gwymo.png)
![\sqrt[3]{16x^(7) * 12x^(9) }](https://img.qammunity.org/2020/formulas/mathematics/middle-school/jf7y9mjxknxgbu5g84glwuthbcvfj16lbk.png) =
=
![\sqrt[3]{16 * 12 * x^(16) }](https://img.qammunity.org/2020/formulas/mathematics/middle-school/d1edrax2aucwidrts8yljzyelknt15o4wm.png)
![\sqrt[3]{16x^(7) * 12x^(9) }](https://img.qammunity.org/2020/formulas/mathematics/middle-school/jf7y9mjxknxgbu5g84glwuthbcvfj16lbk.png) =
=
![\sqrt[3]{192 * x^(16) }](https://img.qammunity.org/2020/formulas/mathematics/middle-school/bk027hvz9p9iq4dtpmvdydsi6xujtl8bz2.png)
Step 3: Rewrite the expression
![\sqrt[3]{192 * x^(16) }](https://img.qammunity.org/2020/formulas/mathematics/middle-school/bk027hvz9p9iq4dtpmvdydsi6xujtl8bz2.png) =
=
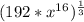
Step 4: Expand the Expression in bracket
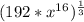 =
=
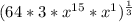
Break down into bits
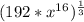 =
=
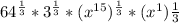
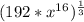 =
=
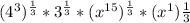
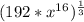 =
=
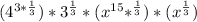
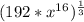 =
=
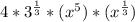
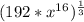 =
=
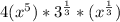
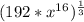 =
=
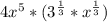
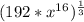 =
=
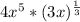
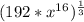 =
=
![4x^(5)} * \sqrt[3]{3x}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/2kiexfgkc3l8eik10b865s1hhclwkuxame.png)
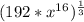 =
=
![4x^(5)} (\sqrt[3]{3x})](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ce97cb7f1g7xdjxxe3htxarltibl2v8vma.png)
Hence, the expression
![\sqrt[3]{16x^(7) } * \sqrt[3]{12x^(9) }](https://img.qammunity.org/2020/formulas/mathematics/middle-school/6ud8ripdrxohsujtf1zr75aw1vidtndz95.png) =
=
![4x^(5)} (\sqrt[3]{3x})](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ce97cb7f1g7xdjxxe3htxarltibl2v8vma.png)