Answer: 56%
Step-by-step explanation:
Given : The selling price of x number of a certain stereo can be modeled by the function :-
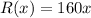
The total cost of making x stereos is :
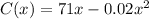
For 31 stereos, the total selling price would be :-
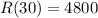
For 31 stereos, the total cost would be :-
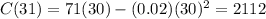
Now, the percent markup will be
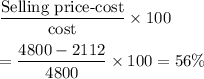
Hence, the percent markup for 31 stereos is 56%.