Answer:
There will be approximately 165,689, 137,264, and 94,207 squirrels in 25, 50, and 100 years respectively.
Explanation:
Exponential Decay Function
The exponential function is often used to model natural growing or decaying processes, where the change is proportional to the actual quantity.
An exponential decaying function is expressed as:
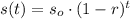
Where:
s(t) is the actual value of the function at time t
so is the initial value of s at t=0
r is the decaying rate, expressed in decimal
The population of squirrels is decreasing at a rate of r=0.75% = 0.0075. The initial number of squirrels is so=200,00. The exponential model for this situation is:
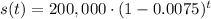
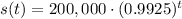
Where s is the number of squirrels at any time t.
We are required to find the number of squirrels in:
t=25 years. Substitute in the formula:
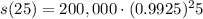
Calculating:
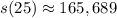
t=50 years. Substitute in the formula:
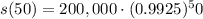
Calculating:
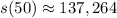
t=100 years. Substitute in the formula:
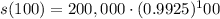
Calculating:
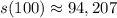
There will be approximately 165,689, 137,264, and 94,207 squirrels in 25, 50, and 100 years respectively.