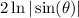Answer:
Proofs are in the explanation.
Explanation:
b) My first thought is to divide top and bottom on the left hand side by
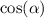 .
.
I see this would give me 1 on top and where that sine is, it would give me tangent since sine/cosine=tangent.
Let's do it and see:
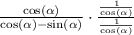
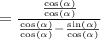
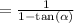
c) My first idea here is to expand the cos(x+y) using the sum identity for cosine.
So let's do that:
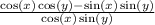
Separating the fraction:
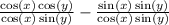
The cos(x) cancel's in the first fraction and the sin(y) cancels in the second fraction:
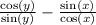

d) This one makes me think it is definitely essential that we use properties of logarithms.
The left hand side can be condense into one logarithm using the product law:
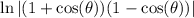
We are multiplying conjugates inside that natural log so we only need to multiply the first and the last:
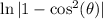
I can rewrite
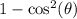 using the Pythagorean Identity:
using the Pythagorean Identity:
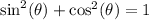 :
:
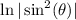
Now by power rule for logarithms: