Answer:
Composition of the mixture:
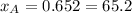 %
%
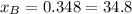 %
%
Composition of the vapor mixture:
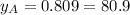 %
%
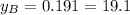 %
%
Step-by-step explanation:
If the ideal solution model is assumed, and the vapor phase is modeled as an ideal gas, the vapor pressure of a binary mixture with
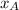 and
and
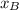 molar fractions can be calculated as:
molar fractions can be calculated as:
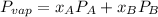
Where
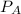 and
and
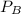 are the vapor pressures of the pure compounds. A substance boils when its vapor pressure is equal to the pressure under it is; so it boils when
are the vapor pressures of the pure compounds. A substance boils when its vapor pressure is equal to the pressure under it is; so it boils when
 . When the pressure is 0.60 atm, the vapor pressure has to be the same if the mixture is boiling, so:
. When the pressure is 0.60 atm, the vapor pressure has to be the same if the mixture is boiling, so:

With the same assumptions, the vapor mixture may obey to the equation:
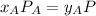 , where P is the total pressure and y is the fraction in the vapor phase, so:
, where P is the total pressure and y is the fraction in the vapor phase, so:
 %
%
The fractions of B can be calculated according to the fact that the sum of the molar fractions is equal to 1.