Question

I need help with these questions. Please assist me.
​

Answer 1

1. True

2.False

3. c

4. d

Answer 2

1) a. True.

2) b. False.

3) b. 1.5

4) a. 80

Explanation:

1. True.

Example the sequence {2,5,8,11,14,...} could be thought of as the set of points:

(1,2) <---Means the first term is 2.

(2,5) <----Means the first term is 5.

(3,8) <----Means the third term is 8.

(4,11) <----Means the fourth term is 11.

(5,14) <----Means the fifth term is 14.

I use this a lot when writing explicit forms for sequences.

The explicit form for this particular sequence is
`a_n=2+3(n-1)` since it is arithmetic with first term 2 and common difference 3; example 5-2=8-5=11-3=14-11 is equal to 3.

This is like saying I have an equation for a line with slope 3 and y-intercept 2-3=-1 (I used the pattern from about to see what would happen at x=0).

We would be able to see this in our equation we wrote if we simplify and put into slope-intercept form:

`a_n=2+3(n-1)`

Distribute:

`a_n=2+3n-3`

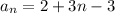
Group 2 and -3 and perform the simplification:

`a_n=2-3+3n`

`a_n=-1+3n`

`a_n=3n-1`

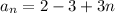
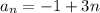
2) False; linear equations are no the only ones that have corresponding sequences. Hopefully another big name in your class is geometric sequences and those correspond to exponential functions. Geometric sequences do have constant base with a exponent as a variable; that makes it exponential. The explicit form for geometric sequences are
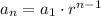`a_n=a_1 \cdot r^(n-1)`. The constant base is r where the exponential variable is n-1.

There are other sequences ,besides arithmetic and geometric. Example, quadratic, cubics, and many others.

3) Geometric sequences have common ratios; what that means no matter what term you choose if you divide by it's previous term, you will get the same thing over and over.

So let's look at we get here when we do term/previous:

3/2=1.5

4.5/3=1.5

6.75/4.5=1.5

So the common ratio is 1.5.

4)
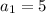`a_1=5` means the first term is 5.

We are given r=2, this is the common ratio.

This means we can keep generating the terms by multiplying by 2.

The first term is 5.

The second term is 5(2)=10.

Third term is 10(2)=20.

Fourth term is 20(2)=40.

Fifth term is 40(2)=80.

If you prefer we could have wrote the explicit form:
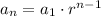`a_n=a_1\cdot r^(n-1)` where
`a_1` is the first term and r is common ratio.

So we have:

`a_n=5 \cdot (2)^(n-1)`

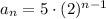
We want the fifth term so replace n with 5:

`a_5=5 \cdot (2)^(5-1)`

`a_5=5 \cdot (2)^4`

`a_5=5 \cdot 16`

`a_5=80`

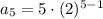
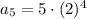
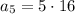
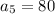
So the fifth term is 80.