Answer:
A.

Explanation:
We have been given a diagram. We are asked to find the measure of angle ABC.
First of all, we will find measure of major arc AC by subtracting 146 from 360 degrees.
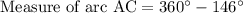

Now, we will use tangent-tangent angle theorem to solve for ABC.
Tangent-Tangent angle theorem states that angle formed by two tangents outside a circle is half the difference of intercepted arcs.
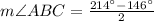


Therefore, the measure of angle ABC is 34 degrees and option A is the correct choice.