2 Answers

Cazort · Answer 1 · 2020-06-07T13:21:48+0000

Answer:

A.
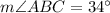
$m\angle ABC=34^(\circ)$

Explanation:

We have been given a diagram. We are asked to find the measure of angle ABC.

First of all, we will find measure of major arc AC by subtracting 146 from 360 degrees.

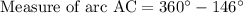
$\text{Measure of arc AC}=360^(\circ)-146^(\circ)$

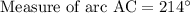
$\text{Measure of arc AC}=214^(\circ)$

Now, we will use tangent-tangent angle theorem to solve for ABC.

Tangent-Tangent angle theorem states that angle formed by two tangents outside a circle is half the difference of intercepted arcs.

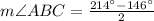
$m\angle ABC=(214^(\circ)-146^(\circ))/(2)$

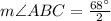
$m\angle ABC=(68^(\circ))/(2)$

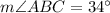
$m\angle ABC=34^(\circ)$

Therefore, the measure of angle ABC is 34 degrees and option A is the correct choice.

Please log in or register to add a comment.