Question

A 4-meter ladder is placed against a wall so

that it reaches a height of 3.7m. To the nearest
tenth of a meter, how far away from the base
of the wall are the feet of the ladder?

Answer 1

1.5 meters.

Explanation:

The ladder is 4 meters.

It reaches the height of 3.7 meters on a wall.

This creates a right angled triangle of hypotenuse (4 meters) and height (3.7 meters).

We are to find the base length.

Applying the Pythagorean theorem;

a² + b² = c² , where a is the base length, b is the height length and c is the hypotenuse length.

∴ a² = c² - b² = 4² - 3.7² = 2.31

a (base length) =
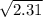`√(2.31)` = 1.519868415 meters

To round off the answer to the nearest tenth of a meter;

Tenth of a meter =
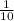`(1)/(10)` × 1 meter = 0.1 meters

So we're rounding off the answer to one decimal place.

I.e 1.519868415 meters = 1.5 meters (rounded off to the nearest tenth of a meter.