Question

Examine this system of equations. Which number can be multiplied by each equation so that when the two equations are

added together, the y term is eliminated?
15 times the first equation and 12 times the second equation
15 times the first equation and -12 times the second equation
30 times the first equation and -6 times the second equation
30 times the first equation and 6 times the second equation

IM BEING TIMED

Answer 1

other dude is right i tested it

Explanation:

Answer 2

15 times the first equation and -12 times the second equation

Explanation:

we have

`(3)/(4)x+(2)/(3)y=6` ------> first equation

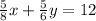`(5)/(8)x+(5)/(6)y=12` ------> second equation

Multiply the first equation by 15 both sides

`(15)(3)/(4)x+(15)(2)/(3)y=6(15)`

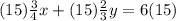
`(45)/(4)x+10y=90` -----> new first equation

Multiply the second equation by -12 both sides

`(-12)(5)/(8)x+(-12)(5)/(6)y=12(-12)`

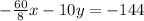`-(60)/(8)x-10y=-144` -----> new second equation

Adds the two new equations

`(45)/(4)x+10y=90\\-(60)/(8)x-10y=-144\\-----------\\(45)/(4)x-(60)/(8)x=90-144`

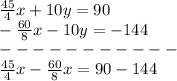
The y-term was eliminated