Answer:
15 times the first equation and -12 times the second equation
Explanation:
we have
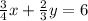 ------> first equation
------> first equation
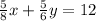 ------> second equation
------> second equation
Multiply the first equation by 15 both sides
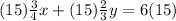
 -----> new first equation
-----> new first equation
Multiply the second equation by -12 both sides

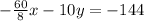 -----> new second equation
-----> new second equation
Adds the two new equations
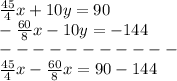
The y-term was eliminated