Question

Write a linear function f with f (5) = -1 and f(0) = -5.
f(x)=____

Answer 1

We conclude that the equation of a linear function with f (5) = -1 and f(0) = -5 will be:

• f(x) = 4/5x - 5

Explanation:

Given

• f(5) = -1

• f(0) = -5

f(5) = -1 means at x = 5, y = -1

Hence, the point (5, -1) lies on the line function.

f(0) = -5 means at x = 0, y = -5

Hence, the point (0, -5) lies on the line function.

Thus, the two points on the linear line function graph are:

• (5, -1)

• (0, -5)

Finding the slope between the points (5, -1) and (0, -5)

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(5,\:-1\right),\:\left(x_2,\:y_2\right)=\left(0,\:-5\right)`

`m=(-5-\left(-1\right))/(0-5)`

`m=(4)/(5)`

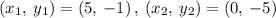
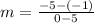
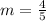
The slope-intercept form of the linear line function

`y = mx+b`

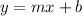
where m is the slope and b is the y-intercept

We have already determined the slope which is: m = 4/5

We know the y-intercept can be determined by setting x = 0 and solving for y.

Thus, the point (0, -5) represents the y-intercept b = -5.

Now, substituting m = 4/5 and b = -5 in the slope-intercept form

`y = mx+b`

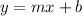
y = 4/5x + (-5)

y = 4/5x - 5

Therefore, we conclude that the equation of a linear function with f (5) = -1 and f(0) = -5 will be:

• f(x) = 4/5x - 5