Answer:
slope =

Explanation:
To find the slope, differentiate with respect to x and evaluate at x = 4
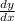 is the measure of the slope of the tangent at x = a
is the measure of the slope of the tangent at x = a
Differentiate each term using the power rule
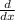 (a
(a
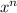 ) = na
) = na
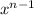
Given
y =
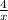 + 2
+ 2
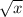
= 4
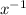 + 2
+ 2
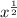 , hence
, hence
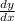 = - 4
= - 4
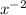 +
+

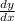 = -
= -
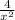 +
+
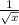
At x = 4
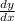 = -
= -
 +
+
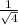
= -
 +
+
 =
=
