Question

The technology company DataGenetics suggests that % of all four-digit personal identification numbers, or PIN codes, have a repeating digits format such as . Assuming this to be true, if the PIN codes of eleven people are selected at random, what is the probability that at least one of them will have repeating digits? Round your answer to four decimal places

Answer 1

Answer: 0.9995

Explanation:

Number of digits to make any code (0 to 9) = 10

If repetition is allowed , then the total number of possible four digits pin codes that can be formed=
`10^4=10,000`

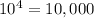
The number of ways to make for digit code without repetition of digits =

`10*9*8*7=5040`

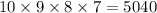
The number of ways to make for digit codes having repetition =

`10,000-5040=4960`

Probability that a person has pin code that has repetition:-

`(4960)/(10,000)=0.496`

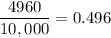
Let x be number of pin codes with repeating digits.

Using binomial probability distribution formula ,

If the PIN codes of seven people are selected at random, then the probability that at least one of them will have repeating digits:-

`P(x\geq1)=1-(P(0))\\\\=1-(^(11)C_0(0.496)^0(1-0.496)^(11))`

`=1-((0.496)^0(0.504)^(11))=0.999466989333\approx0.9995`

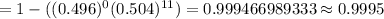
Hence, the probability that at least one of them will have repeating digits = 0.9995