Answer: 0.9995
Explanation:
Number of digits to make any code (0 to 9) = 10
If repetition is allowed , then the total number of possible four digits pin codes that can be formed=
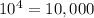
The number of ways to make for digit code without repetition of digits =
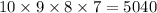
The number of ways to make for digit codes having repetition =
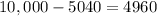
Probability that a person has pin code that has repetition:-
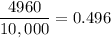
Let x be number of pin codes with repeating digits.
Using binomial probability distribution formula ,
If the PIN codes of seven people are selected at random, then the probability that at least one of them will have repeating digits:-
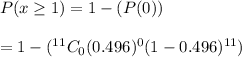
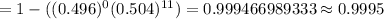
Hence, the probability that at least one of them will have repeating digits = 0.9995