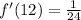Question

Find the derivative of f(x) = negative 6 divided by x at x = 12.

Answer 1

1/24

Explanation:

`f(x)=(-6)/(x)`

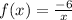
We want to find the derivative of f at x=12.

I'm assuming you want to see the formal definition of a derivative approach.

The definition is there:

`f'(x)=\lim_(h \rightarrow 0)(f(x+h)-f(x))/(h)`

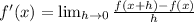
So we need to find f(x+h) given f(x).

To do this all you have to is replace old input, x, with new input, (x+h).

Let's do that:

`f(x+h)=(-6)/(x+h)`.

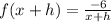Let's go to the definition now:

`f'(x)=\lim_(h \rightarrow 0)(f(x+h)-f(x))/(h)`

`f'(x)=\lim_(h \rightarrow 0)((-6)/(x+h)-(-6)/(x))/(h)`

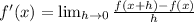
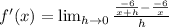
Multiply top and bottom by the least common multiple the denominators of the mini-fractions. That is, we are going to multiply top and bottom by x(x+h):

`f'(x)=\lim_(h \rightarrow 0)((-6)/(x+h)x(x+h)-(-6)/(x)x(x+h))/(hx(x+h))`

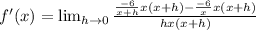
Let's cancel the (x+h)'s in the first mini-fraction.

We will also cancel the (x)'s in the second-mini-fraction.

`f'(x)=\lim_(h \rightarrow 0)(-6x--6(x+h))/(hx(x+h))`

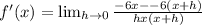
--=+ so I'm rewriting that part:

`f'(x)=\lim_(h \rightarrow 0)(-6x+6(x+h))/(hx(x+h))`

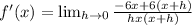
Distribute (NOT ON BOTTOM!):

`f'(x)=\lim_(h \rightarrow 0)(-6x+6x+6h)/(hx(x+h))`

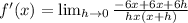
Simplify the top (-6x+6x=0):

`f'(x)=\lim_(h \rightarrow 0)(6h)/(hx(x+h))`

Simplify the fraction (h/h=1):

`f'(x)=\lim_(h \rightarrow 0)(6)/(x(x+h))`

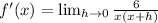
Now you can plug in 0 for h because it doesn't give you 0/0:

`(6)/(x(x+0))`

`(6)/(x^2)`

`f'(x)=(6)/(x^2)`

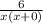
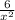
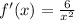
We want to evaluated the derivative at x=12 so replace x with 12:

`f'(12)=(6)/(12^2)`

`f'(12)=(6)/(144)`

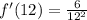
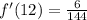
Divide top and bottom by 6:

`f'(12)=(1)/(24)`

Answer 2

1/24

Explanation:

f(x) = -6/x

I will rewrite this as

f(x) = -6 x^-1

We know the derivative of x^-1 is -1 x^ (-1-1) or -1 x^-2

df/dx = -6 * -1 x ^ -2

df/dx = 6 x^-2

df/dx = 6/x^2

Evaluated at x=12

df/dx = 6/12^2

=6/144

=1/24