A hot-rolled steel has a yield strength of Syr-Sye-170 kpsi and a true strain at fracture of 0.55. Estimate the factor of safety for the following stress state, by using a) the …

Question

asked Jan 20, 2020 87.1k views

1 Answer

Diego Aguado · Answer 1 · 2020-01-24T18:01:59+0000

Answer:

a) Factor of safety ≤ 1.689

b) Factor of safety ≤ 1.944

Step-by-step explanation:

Given data:

Yield strength,
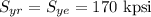
$S_(yr)=S_(ye)=170\ \textup{kpsi}$

True strain factor = 0.55

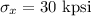
$\sigma_x=30\ \textup{kpsi}$

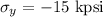
$\sigma_y=-15\ \textup{kpsi}$

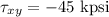
$\tau_(xy)=-45\ \textup{kpsi}$

Now, principle stress is given as:

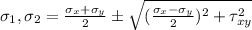
$\sigma_1,\sigma_2 = (\sigma_x+\sigma_y)/(2)\pm\sqrt{((\sigma_x-\sigma_y)/(2))^2+\tau_(xy)^2$

on substituting the values we get

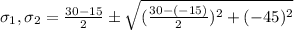
$\sigma_1,\sigma_2 = (30-15)/(2)\pm\sqrt{((30-(-15))/(2))^2+(-45)^2$

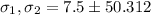
$\sigma_1,\sigma_2 =7.5\pm50.312$

or

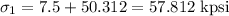
$\sigma_1 =7.5+50.312=57.812\ \textup{kpsi}$

and

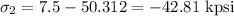
$\sigma_2 =7.5-50.312=-42.81\ \textup{kpsi}$

a) By maximum shear stress theory

we have

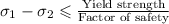
$\sigma_1-\sigma_2\leqslant \frac{\textup{Yield\ strength}}{\textup{Factor\ of\ safety}}$

on substituting the values, we get

$57.812-(-42.81)\leqslant\frac{170}{\textup{Factor\ of\ safety}}$

or

Factor of safety ≤ 1.689

b) By the distortion energy theory

$(1)/(2)[(\sigma_1-\sigma_2)^2+(\sigma_2-\sigma_3)^2+(\sigma_3-\sigma_1)^2]\leqslant\frac{S_(yr)}{\textup{Factor\ of\ safety}}$

since no force is acting in the z- direction, thus
$\sigma_3 = 0$

on substituting the values, we get

$(1)/(2)[(30-(-15))^2+(-15-0)^2+(0-30)^2]\leqslant\frac{170}{\textup{Factor\ of\ safety}}$

or

Factor of safety ≤ 1.944