Answer:
a) Factor of safety ≤ 1.689
b) Factor of safety ≤ 1.944
Step-by-step explanation:
Given data:
Yield strength,
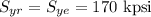
True strain factor = 0.55
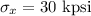
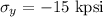
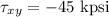
Now, principle stress is given as:
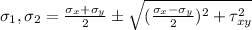
on substituting the values we get
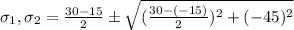
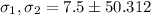
or
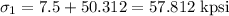
and
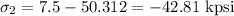
a) By maximum shear stress theory
we have
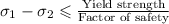
on substituting the values, we get
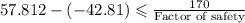
or
Factor of safety ≤ 1.689
b) By the distortion energy theory
![(1)/(2)[(\sigma_1-\sigma_2)^2+(\sigma_2-\sigma_3)^2+(\sigma_3-\sigma_1)^2]\leqslant\frac{S_(yr)}{\textup{Factor\ of\ safety}}](https://img.qammunity.org/2020/formulas/physics/college/1ag0dsbg25ghifu7e1fjm4qs50kt3ri40v.png)
since no force is acting in the z- direction, thus
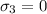
on substituting the values, we get
![(1)/(2)[(30-(-15))^2+(-15-0)^2+(0-30)^2]\leqslant\frac{170}{\textup{Factor\ of\ safety}}](https://img.qammunity.org/2020/formulas/physics/college/4yukmxgaa98ujogpi3d1mzqqgfjfn1s0hp.png)
or
Factor of safety ≤ 1.944