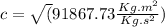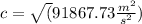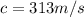Answer:
The speed of the sound for the adiabatic gas is 313 m/s
Step-by-step explanation:
For adiabatic state gas, the speed of the sound c is calculated by the following expression:
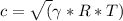
Where R is the gas's particular constant defined in terms of Cp and Cv:
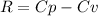
For particular values given:
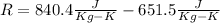
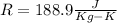
The gamma undimensional constant is also expressed as a function of Cv and Cp:
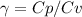
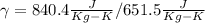
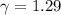
And the variable T is the temperature in Kelvin. Thus for the known temperature:
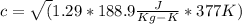

The Jules unit can expressing by:
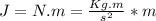
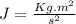
Replacing the new units for the speed of the sound: