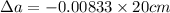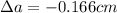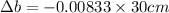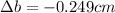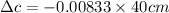Question

A rectangular block having dimensions 20 cm X 30 cm X 40 cm is subjected to a hydrostatic stress of -50 kPa (i.e. under compression). Calculate the change in length of each side. Data: Young's modulus of the block E = 600 kPa, Poisson ratio v=0.45.

Answer 1

`\Delta a=-0.166 cm`

`\Delta b=-0.249 cm`

`\Delta c=-0.332 cm`

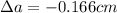
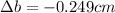
Step-by-step explanation:

Given that E=600 KPa

Poisson ratio=0.45

We know that for hydroststic stress ,strain given as

`\varepsilon =(\sigma)/(E)(2\mu -1)`

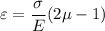
Here given that
`\sigma =-50 KPa`

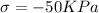
Now by putting the values

`\varepsilon =(50)/(600)(2* 0.45 -1)`

`\varepsilon =-0.00833`

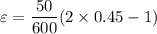
Negative sign indicates that dimensions will reduces due to compressive stress

We know that strain given as

`\varepsilon =(\Delta L)/(L)`

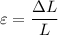
Lets take a=20 cm,b=30 cm,c=40 cm.

So
`\Delta a=-0.00833* 20 cm`

`\Delta a=-0.166 cm`

`\Delta b=-0.00833* 30 cm`

`\Delta b=-0.249 cm`

`\Delta c=-0.00833* 40 cm`

`\Delta c=-0.332 cm`