Answer:
The 4th side on quadrilateral ABCD is
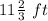
Explanation:
we know that
If two figures are similar, then the ratio of its corresponding sides is proportional and this ratio is called the scale factor
In this problem
The corresponding sides are
ABCD EFGH
20 ft ?
18 ft ?
14 ft 6 ft
? 5 ft
The length side of 14 ft in quadrilateral ABCD is the corresponding side to the length side of 6 ft in quadrilateral EFGH
so
the scale factor from quadrilateral ABCD to quadrilateral EFGH is
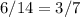
therefore
To find the length of the 4th side on quadrilateral ABCD, divide the length of the 4th side on quadrilateral EFGH by the scale factor
so
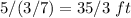
convert to mixed number
