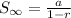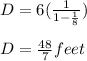Question

A ball is dropped and begins bouncing. On the first bounce, the ball travels 3 feet. Each consecutive bounce is 1/8 the distance of the previous bounce. What is the total distance that the ball travels? Round to the nearest hundredth.

Answer 1

Total distance covered equals
`(48)/(7)feet`

Step-by-step explanation:

The situation is represented in the attached figure

Distance in first bounce =
`d_(1)=2* 3ft`

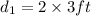
Distance in second bounce =
`d_(2)=2* (3)/(8)ft`

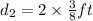
Distance in third bounce=
`d_(3)=2* (3)/(8^(2))ft`

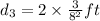
Thus the total distance covered =
`d_(1)+d_(2)+d_(3)+...`

Applying values we get

Total distance covered =
`2* 3+2* (3)/(8)+2* (3)/(8^(2))+2* (3)/(8^(3))+....\\\\=6(1+(1)/(8)+(1)/(8^(2))+(1)/(8^(3))+...)`

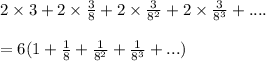
Summing the infinite geometric series we get total distance covered as
`S_(\infty )=(a)/(1-r)`

`D=6((1)/(1-(1)/(8)))\\\\D=(48)/(7)feet`